The color of soap bubbles
Where does the color of the bubbles come from?

Take an extra look into the phenomenon behind the colors of soap bubbles

Where does the color of the bubbles come from?
This page is based on the basic page The color of soap bubbles. So if you have not read it yet, it might be a good idea to start with the link to the right :)
The reflection intensity from a soap film for light of a given wave length can be calculated by using this formula (source is Cyril Isenbergs great book, "The Science of Soap films and Soap bubbles":
The reflection intensity
where is the intensity of the incoming ray of light, is the maximum reflection intensity from the film, is the wavelength of the given ray of light, is the refractive index of the film, is the thickness of the film, and is the angle of the refracted light with regards to the normal of the film.
The graph below illustrates how the interference of one color (yellow with wave length 589 nm, which is the same as the light from a low pressure sodium lamp) depends on the thickness of a soap film.
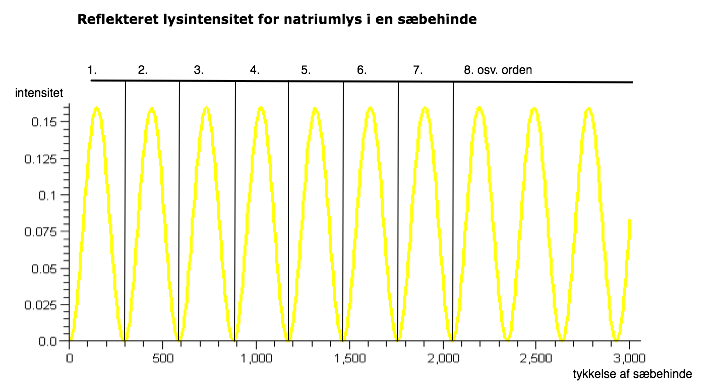
Intensity of the reflected light from a sodium lamp in a soap film
We say that there is a so-called order between two troughs in the wave pattern of a repeated color spectre. The light intensity within one order therefore varies from total destructive interference over total constructive interference to total destructive interference again, where the next order start. According to the graph above the with of an order corresponds to ca. half the wave length (589 nm). An explanation for this is that the light has to move both back and forth in the film and optical path therefore corresponds to ca. two times the film thickness. Notice that the first total destructive interference happens when the soap film is 0 nm thick. Below is picture of a bubble illuminated by a low pressure sodium lamp. A close up is presented for one of the orders.

Soap bubble dome on a light table illuminated by monochromatic light
The reflection intensity of the order is most powerfull just below the middle of the height and dampens the nearer we get to the neighbouring orders.
Here is a closeup of the lower part of the bubble and a photo with indicators of the soap film thickness.

Close up of of a soap bubble dome on a light table illuminated with monochromatic light and indicated thickness in nm
Even at relatively high magnification it can be difficult to estimate the number of orders at the bottom of a soap film. However, there seem to be around 11 orders, i.e. 10 black stripes in the dome above. From the graph of intensity versus soap film thickness above, the estimated soap film thickness at the bottom is around 3000 nm. Notice that the orders becomes more narrow when moving downwards. This shows that the thickness of the bubble is not changing linearly along the film as the tangent of the bubbles goes towards vertical when moving downwards along the film.
We have now seen that a soap film reflects light of one wavelength as alternating belts of the color and black as a visualisation of constructive and destructive interference. This pattern is valid for light colors (wave lengths), however, the width and location of the belts change with the wave length. Light with a longer wavelengths have wider orders than light with shorter wavelengths.
As previously described, white light (from the sun or from an incandescent bulb) consists of the full spectrum of visible wave lengths from violet to red. When we describe white light we can think of it as several monochrome light wave, and we can use the same equation as for the yellow light above on each wave length. Below we present the reflection intensities as funktion of the soap film thickness for the wave lengths normally perceived as violet, blue, green, yellow, orange, and red.
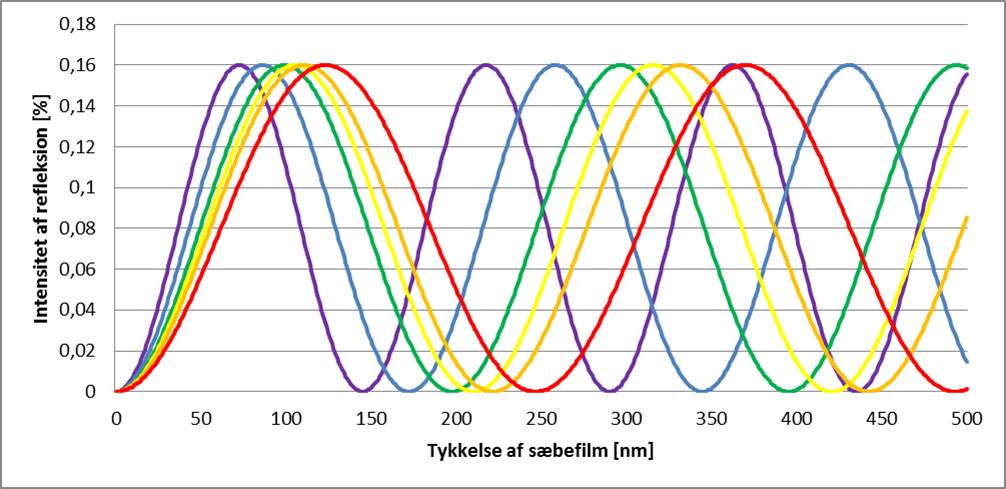
Reflection intensity from soap film for different wave lengths
It is then possible to estimate the color of the soap film at a specific thickness by adding up the contribution from each of the colors. The color as a function of film thickness can be found in the table below from [source Cyril Isenberg "The Science of Soap Bubble and Soap films"].
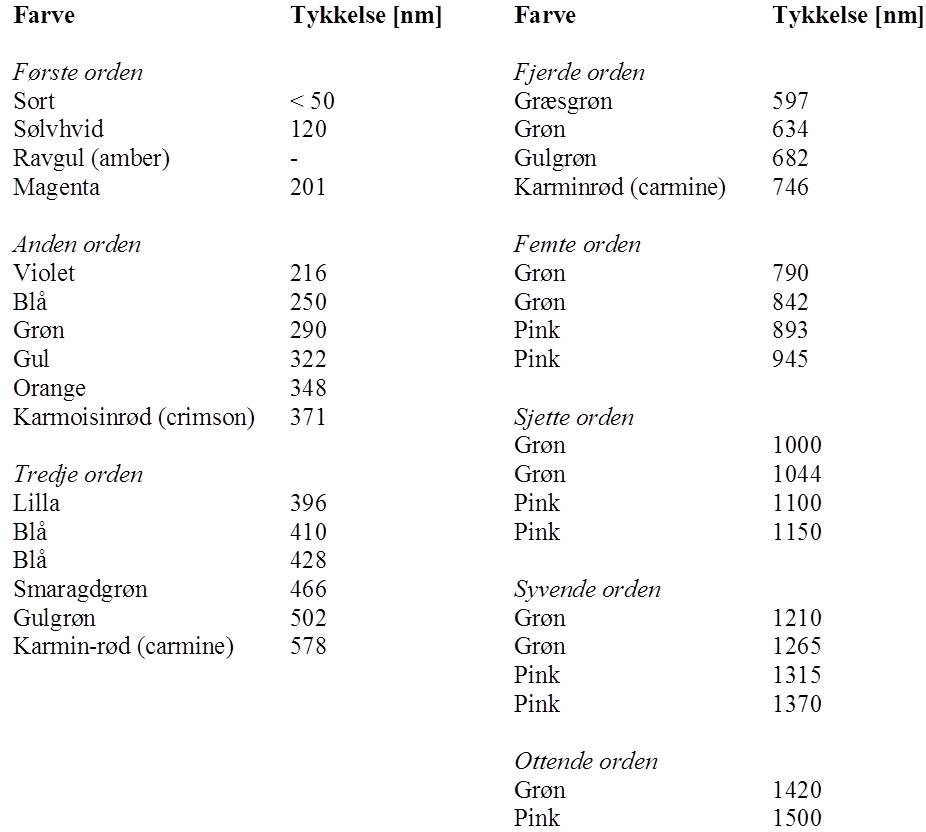
Color of the reflected light as a function of the film thickness [Isenberg, 1992]

Soap film illuminated by white light with estimated thicknesses
For very thin soap films all wave lengths will be reflected almost equally and the soap film will therefore be perceived as silvery white. This happens from film thicknesses of about 120 nm down to about 30 - 50 nm. From thicknesses of about 30 - 50 nm and thinner the soap film will be almost invisible and form of a so called black film. It is said that the black film is one of the thinnest phenomenons visible by the human eye.

Thin soap film with black film
According to plot above a (theoretical) film of 0 nm will result in total destructive interference for all wave lengths. This is due to the phase shift at the reflection in the surface of the film (point A). Thereby the first reflection gets the opposit phase compared to the other ray exiting the film at C. Therefore they will interfere destructively for all wavelengths. Notic that the waves have not been shifted further since the thickness of the film is 0 nm.
Due to the destructive interference for all wavelengths the black film is perceived as transparent. To best see the colors of soap bubble, it is good to use a light table in a very dark room or with a black background. This is why a black film appears black, hence the name. A soap film of about 30 - 50 nm is called a common black film and a film of about 5 nm (which is aproximatly the minimum soap film thickness) is called a Newton black film [Isenberg, 1992].